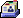Here's a solution to Andy101's which doesn't use the symmetry condition. Label the rows by A through E, the columns by 1 through 5.
Click here to view the secret text
×
First note that there are no mines in B5, C4, D4, or D5. Note also that A5+B5=2 regardless of whether there's a mine in A5. We'll show there must be a mine in E5. Indeed, if there isn't, then D5 and E5 would be the same, either 0 or 1 depending on whether E4 is a mine, and then the last column wouldn't sum to 4. Thus E5 must be a mine.
To get the last column to sum to 4, we must have D5=1, so there is no mine in E4. Now consider C4+D4+E4, which we want to be 7. Right now, each of these squares is adjacent to one mine, so we need them to be adjacent to four more. If there is a mine at B3, C3, D3, or E3, this will add 1, 2, 3, or 2 to this total respectively. Therefore either C3 and E3 are mines or B3 and D3 are. The first case is impossible because then the row D adds up to more than 4, so there are mines in B3 and D3. It also follows that there is no mine in A3 or A5.
Suppose there no mine in D2. Then since row D sums to 4, D2=1. But then there are no mines in D1, E1, or E2, and this is bad for the row E sum. Thus there's a mine in D2. Then we must have D1=1. From here we deduce that row C has no mines and no other mines border it, and the rest is easy.